Suffix Automoton 学习笔记

首先日膜foin生鲜

我是在太菜了Uncle SAM 学了第二遍才懂

如果想在一个有向无环图中表示一个字符串的字串，必须满足一下四条性质：

• 有一个源点，许多个终止点，其中每条边上都有一个字符，从源点到任意一个终止点的路径上的边能构成一个字符串。
• 对于这一个源点，到任意一个节点的路径上所组成的字符串，均为原串的子串，任意一个不能表示为源点到一个节点上路径组成的字串的字符串，均不为原串的字串。即每一个原串的字串，与源点到每一个节点的路径一一对应。
• 对于源点，到每一个终止节点的路径形成的字符串均为原串的后缀。
• 对于源点，到任意一个节点的路径所形成的字符串两两不同。

显然 Trie 树完全可以满足这个要求.

以字符串”AKIOI”为例，将其后缀 “I”, “OI”, “IOI”, “KIOI”,”AKIOI” 依次加入即可得到下图的字典树, 其中蓝点为源点，黄点为终止点。

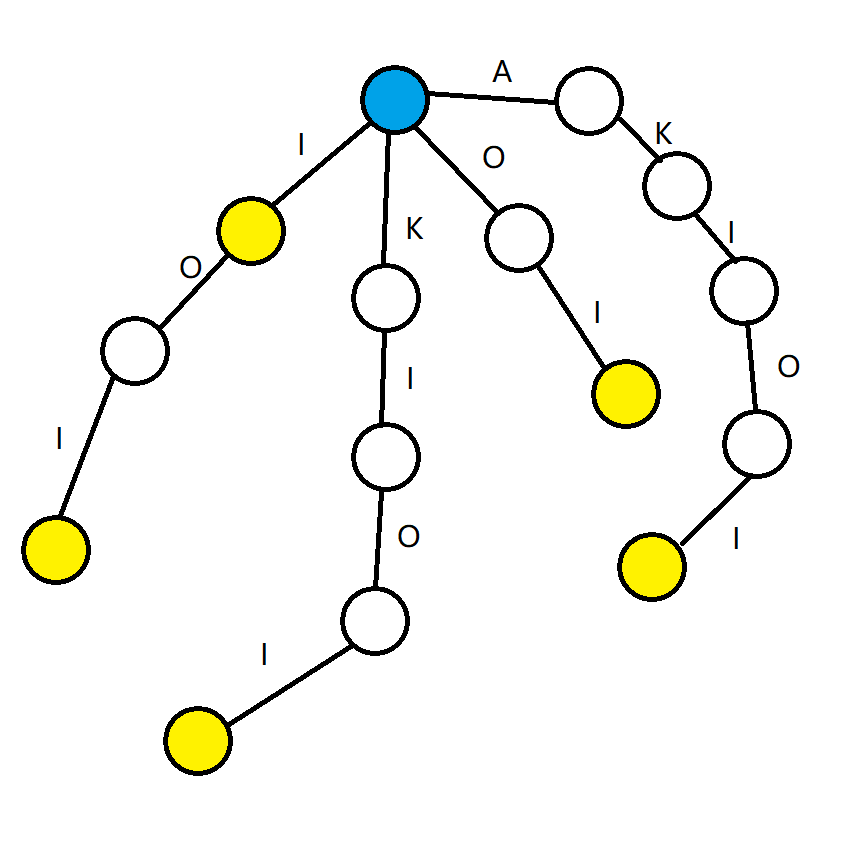
但是它有许多重复的、可以合并的节点，导致了它的节点数量是$\Theta(n^2)$级别的。所以，需要构造一个节点数量、边数量尽可能少的一个DAG满足以上四个要求。

SAM的性质

• 对于一个字串$p$，可能出现在原串的若干个位置。由所有出现位置的右端点的编号组成的几何，定义为$\text{endpos(p)}$，例如对于字符串”LSWNWNWNAKWNIOI”, $\text{endpos}(\text{WN})=\{4,6,8,12\}$。
• 对于所有的 endpos ​值相同的字符串，将这些字符串归为一个endpos等价类。

那么易得下面三个结论：

• 1.对于字符串$s$和字符串$t$，且$|S|\leq|T|$若$\text{endpos} (s)=\text{endpos}(t)$，那么$s$为$t$的后缀。

• 2.对于字符串$s$和字符串$t$，且$|S| \leq |T|$要么$\text{endpos}(s) \subseteq \text{endpos}(t)$，要么$\text{endpos}(s)\cup \text{endpos}(t)= \varnothing$

• 3.对于所有的 endpo s等价类，将其中的字符串按照长度排序，排序后为$a_{1},a_{2} \cdots, a_{n}$, 满足$|a_{i+1}-a_{i}|=1, i=1,2,\cdots,n-1$。

同时也可以得到下面两个个结论：

• 4.endpos 等价类的数量是$\Theta(n)$级别的，在下面的证明中，将 endpos 等价类简称为类。

  证明：对于一个类中最长的字符串$p$,如果在$p$前添加任意一个字符，并且保证新形成的字符串$s$仍然为原串的字串，那么有$\text{endpos}(s)\subseteq \text{endpos}(p)$。同时，如果在$p$前添加另外一个字符，保证新形成的字符串$r$也为原串的字串，那么也有$\text{endpos}(r)\subseteq \text{endpos}(p)$，但是显然有$\text{endpos(r)} \cup \text{endpos(s)} = \varnothing$，同时$s$和$t$不属于这个类。将所有如同$s$,$t$的字符串取出，组成一个集合$add$。那么每个字符串都在一个新的类中，且每个字符串的$endpos$值都是$\text{endpos}(p)$的子集，并且$\forall a,b \in add, \text{endpos}(a) \cup \text{endpos}(b)=\varnothing$。所以，相当于把原集合分割成若干个集合，并且保留原集合，那么因为每个$endpos$都是从$\{1,2,3 \cdots,n\}$中分割出来的，所以$endpos$等价类的个数为$\Theta(n)$级别的。得证。分割的过程如下图。这棵树有一个睿智的名字，叫Parent Tree.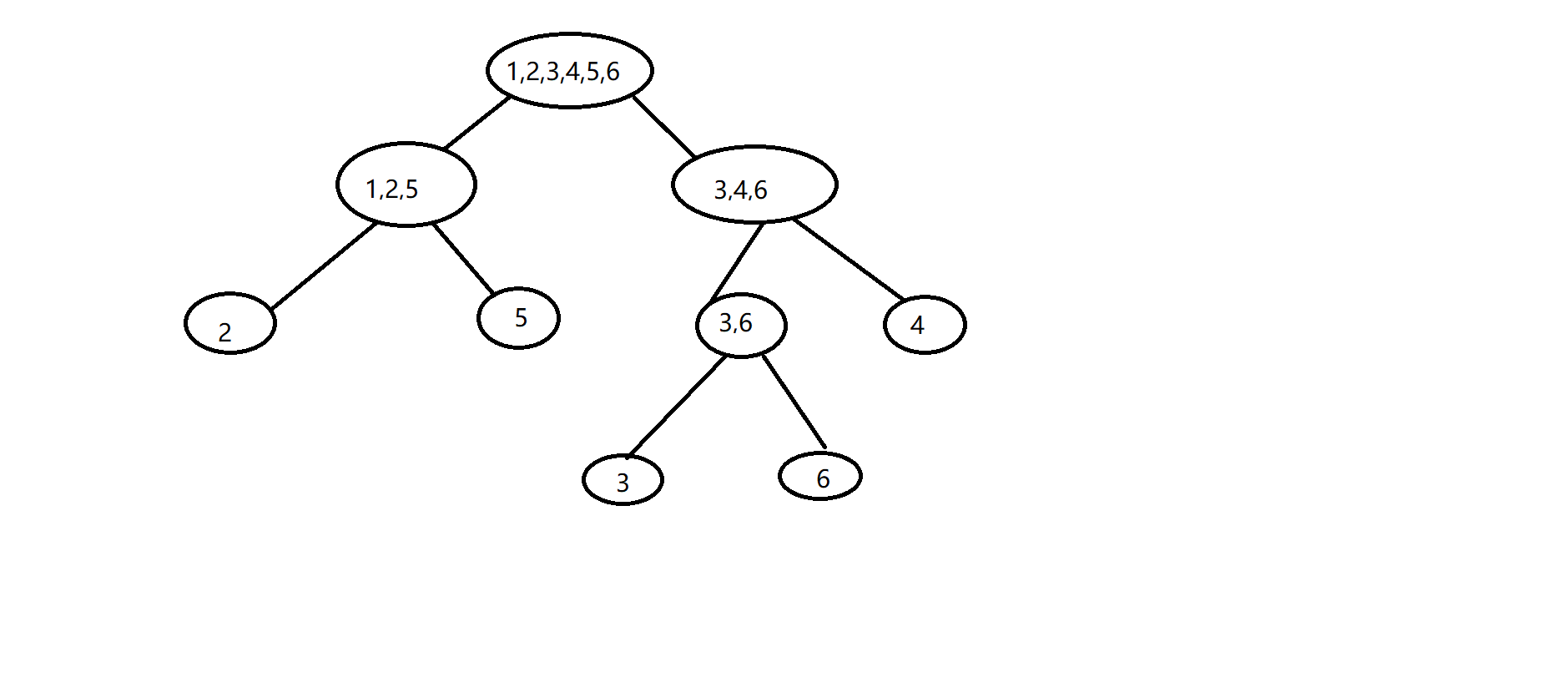

  

• 5.对于一个 endpos 等价类$a$，既有最长字串，又有最短字串。定义其在 Parent Tree 中的父亲等价类为$\operatorname{fa}(a)$,定义$a$中最长字符串的长度为$\text{maxlen}(a)$,定义$a$中最短字符串的长度为$\text{minlen}(a)$。那么$\text{maxlen}(\text{fa}(a))+1=\text{minlen}(a)$。这个结论非常容易得到。下面以字符串 “LLSLSL” 为例子画出整个 parent tree 。

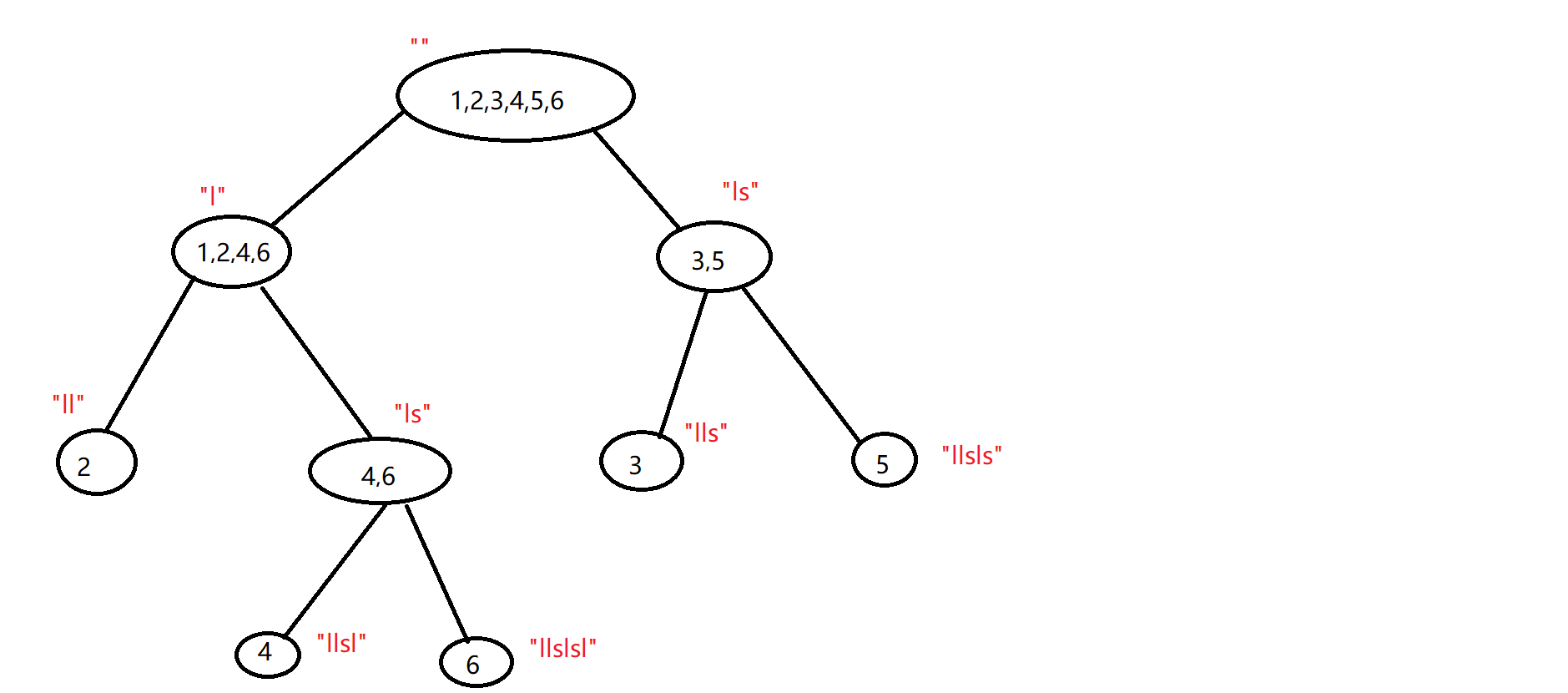
  而SAM就是在Parent Tree上建成的，SAM上的节点就是 Parent Tree 上的节点，只是其中的边连的有所不同。其中空串所属节点就是SAM的源点，终止节点就是原串所在节点。

所以我们只要在Parent Tree上连一些边，使得从源点开始到任意节点$i$的路径上形成的字符串均为该节点$i$所代表的 endpos 等价类。于是只需要证明后缀自动机的边数为$\mathcal O(n)$量级的就可以了。~~但是我真的懒得证了，所以我们不妨假设是这样的。

所以，总结一下：对于一个字符串 $S$， 它的 SAM 是一个能够识别，且仅能够识别 $S$ 的所有后缀的自动机。 即 $\text{SAM}(x)=True$，当且仅当 $x$ 为$S$ 的后缀。

一些定义

对于一个自动机 $K$， 如果 $K$ 能够识别字符串 $S$， 那么记为 $K(S)=True$，否则 $K(S)=False$。

$\text{trans}(x,ch)$为 $x$ 状态下读入字符 $ch$ 所达到的状态。如果这个状态不存在，记为 $\text{trans}(x,ch)=\text{NULL}$。其中$\text{NULL}$表示不存在的状态，$trans(\text{NULL},ch)=\text{NULL}$。

$\text{trans}(x,str)$定义为在 $x$ 状态下读入字符串 $str$ 而到达的状态。伪代码如下：

trans(x, str)
	pos = x
	for i = 1 to length of str
		ch = the ith character of str
		pos = trans(pos, ch)
	return pos

那么对于一个自动机 $K$，它所能识别的字符串 $str$ 就是所有使得 $\text{trans}(init, str) \subset end$ 的字符串。那么记作 $\text{Reg}(K)$。同时，从状态 $s$ 开始能够被识别的字符串集合记作 $\text{Reg}(s)$。

SAM 的实现

终于，一堆无聊的废话终于过去了，终于可以上代码了。